Irreversibility
against thermodynamics !
In thermodynamic laws considerations about
process
mechanisms have no significance. The position of equilibriums are
calculated
by comparison of states with reference to energy and entropy
aspects. Thermodynamics describe not the motion of single
atoms/molecules. However, the very large number of atom/molecule
processes results the thermodynamic equilibrium. That's why the
influence of such elemetary processes will here discussed.
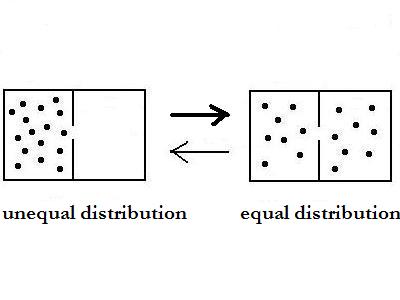
In the picture are two different states with
equal or
unequal distribution. The thermodynamic logic says, that the equal
state has a higher probability than the unequal. But as
simple true it seems , as wrong it is!
States have not a probabilty!
Only processes have a probability.
In this case it is correct to say, that the process
from unequal to equal distribution has a higher probability than the
opposite one. This is simple but very
important.
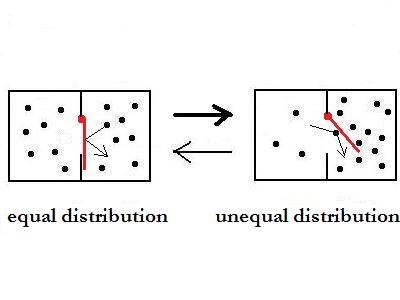
By addition of the red plank, which can swing
only in one direction, the circumstances are very different. The
plank causes, that the motion process from left to right as a higher
probability than the opposite one. The plank process is an irreversible
one, because a single ball can only push it open from left to
right.
The mistake, that states haven't a probability, makes a great
difference here. In equilibrium, there is not an equal but an unequal
distribution, although the energy and entropy circumstances are the
same like in the first picture 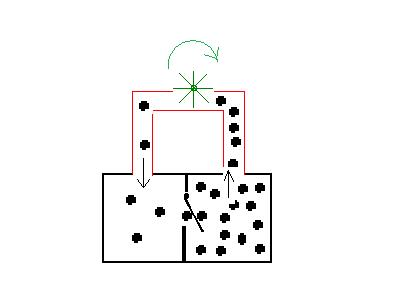
Equilibriums, created by irreversible
elementary processes, are in thermodynamic calculations non
equilibriums. But with a thermodynamic non equilibrium it is possible
to produce mechanical motion, symbolized by the wheel. It is a
perpetual motion machine of second kind. Other examples of this principle are the Dropping funnel and the Brownian ratchet .
Systems, determined by reversible processes, can be
calculated by themodynamic laws. But in systems with irreversible
processes, the mistake, that states haven't a probability, make the
differece. In such systems the second law of thermodynamics has not
validity. Levenspiel's fountain is an example to this principle.
The importance of this principle to living systems is discussed in the
link principle of live
.
back
next